2021-11-30, სამშაბათი

ტრიგონომეტრიული დავალებები ეროვნული გამოცდის ტესტებიდან.

იპოვეთ სწორი პასუხები:

2018.17. იპოვეთ sin⁴a+cos⁴a, თუ sina.cosa=m

1. (1-m)²
2. (1+m)²
3. m²+1
4. 1-2m²

2018.28. y=cos(x-3) ფუნქციის გრაფიკი სიმეტრიულია:

1. ორდინტთა ღერძის მიმართ;
2. (3; 0) წერტილის მიმართ;
3. x=3 განტოლებით განსაზღვრული წრფის მიმართ;
4. y=3 განტოლებით განსაზღვრული წრფის მიმართ.

2019.17. ქვემოთ ჩამოთვლილი შუალედებიდან რომელს ეკუთვნის arccos(-1/4)?

1. (-π; - π/2)
2. (-π/2; 0)
3. (0; π/2)
4. (π/2; π)

2019.28. f(x)=cos(6x+1) ფუნქციის უმცირესი დადებითი პერიოდი ტოლია:

1. π/3
2. π/3 + 1
3. π/3 – 1
4. 2π + 1

2020.22 (ვარ.1). სურათზე გამოსახულია [0; 2π] შუალედზე განსაზღვრული f(x)=asinx და g(x)=b+cosx ფუნქციების გრაფიკები, სადაც a და b ნამდვილი რიცხვებია. სურათის მიხედვით იპოვეთ a+b გამოსახულების მნიშვნელობა.

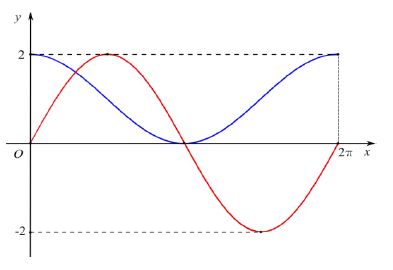
1. 4
2. 3
3. 2
4. 1

2020.22 (ვარ.2). სურათზე გამოსახულია [0; 2π] შუალედზე განსაზღვრული f(x)=acosx და g(x)=b+sinx ფუნქციების გრაფიკები, სადაც a და b ნამდვილი რიცხვებია. სურათის მიხედვით იპოვეთ a-b გამოსახულების მნიშვნელობა.

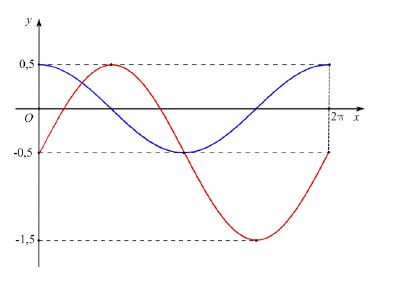
1. -1
2. 1,5
3. 1
4. 0

2020.25 (ვარ.1). ABC მახვილკუთხა სამკუთხედზე შემოხაზულია წრეწირი, რომლის ცენტრია O წერტილი, ხოლო რადიუსი R-ის ტოლია.იპოვეთ AC გვერდის სიგრძე, თუ კუთხე OAB = α და კუთხე OCB=β

1. 2Rcos(α+β)
2. Rsin(α+β)
3. 2Rsinαsinβ
4. 2Rsin(α+β)

2020.28 (ვარ.1). იპოვეთ sin(πx/6)=1/2 განტოლების [0; 15] შუალედში მოთავსებული ამონახსნების ჯამი.

1. 6
2. 16
3. 19
4. 20

2020.28 (ვარ.2). იპოვეთ cos(πx/3)=1/2 განტოლების [0; 9] შუალედში მოთავსებული ამონახსნების ჯამი.

1. 6
2. 13
3. 15
4. 18

2021.22 (ვარ.1). გამოთვალეთ sin(2α), თუ ცნობილია, რომ 90° < α < 270° და sinα=1/3.

1. -4√2/9
2. -2√2/9
3. 4√2/9
4. 2/3

2021.22 (ვარ.2). გამოთვალეთ cosα, თუ ცნობილია, რომ 90° < α < 270° და tgα=1/5.

1. -5/√26
2. -1/√26
3. -√3/5
4. 1/√26

2021.22 (ვარ.3). იპოვეთ tgα, თუ (sinα-cosα)/(2sinα + 3cosα)=2

1. -7/3
2. -2/5
3. 1/3
4. 1/2

ამოხსენით ამოცანები:

2020.33 (ვარ.2). იპოვეთ ABC მართკუთხა სამკუთხედში უმცირესი კუთხის სინუსი, თუ კუთხე c = 90°, AC=2√3 და BC=3.

2020.33 (ვარ.1). იპოვეთ ABC მართკუთხა სამკუთხედში უმცირესი კუთხის ტანგესი, თუ კუთხე c = 90°, AB=2√5 და BC=4.

2020.40 (ვარ.1). სიბრტყეზე განვიხილოთ ყველა ტოლფერდა ტრაპეცია, რომელთა მახვილი კუთხეა α და ფართობია 10სმ². ამ ტრაპეციების პერიმეტრებს შორის იპოვეთ უმცირესი, თუ sinα=1/5.

2021.33 (ვარ.1). ABC ტოლფერდა სამკუთხედის AB ფუძე π სიბრტყეზე მდებარეობს, ხოლო სამკუთხედის სიბრტყე π სიბრტყესთან α სიდიდის ორწახნაგა კუთხეს ადგენს. იპოვეთ AC ფერდის მიერ π სიბრტყესთან შედგენილი კუთხის სინუსი, თუ AB=m, AC=n.