ვიტყვით, რომ რიცხვი დაშლილია მარტივ მამრავლებად, თუ იგი წარმოდგენილია მარტივ რიცხვთა ნამრავლის სახით. შეიძლება ვაჩვენოთ, რომ ნებისმიერი შედგენილი რიცხვი იშლება მარტივ მამრავლებად და ეს დაშლა ერთადერთია.

შედგენილი რიცხვის მარტივ მამრავლებად დასაშლელად საჭიროა გავყოთ ეს რიცხვი უმცირეს მარტივ გამყოფზე, მიღებულ განაყოფს მოვექცეთ ანალოგიურად და ა. შ., ვიდრე განაყოფში არ მივიღებთ 1-ს. მაგალითად:

420:2=210, 210:2=105, 105:3=35, 35:5=7, 7:7=1.

მარტივ მამრავლებად დაშლის ალგორითმი მოსახერხებელია ჩაიწეროს შემდეგნაირად:

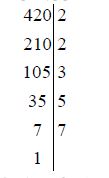
სადაც ვერტიკალური ხაზის მარჯვნივ გვაქვს საძიებელი მარტივი მამრავლები. ამრიგად, დაშლას ექნება სახე: 420 = 2 ⋅ 2 ⋅ 3 ⋅ 5 ⋅ 7.

რამდენიმე ნატურალური რიცხვის საერთო გამყოფი ეწოდება რიცხვს, რომელიც თითოეული მათგანის გამყოფს წარმოადგენს. მაგალითად:

18-ის, 24-ისა და 36-ის საერთო გამყოფებია: 1, 2, 3 და 6.

m, n, ..., k ნატურალური რიცხვების უდიდესი საერთო გამყოფი ეწოდება მათ საერთო გამყოფებს შორის უდიდესს და D(m, n, ..., k) სიმბოლოთი აღინიშნება.

განსახილველი რიცხვების საერთო გამყოფთა სიმრავლე წარმოადგენს მათ გამყოფთა სიმრავლეების თანაკვეთას; ეს სიმრავლე სასრულია და მისი უდიდესი ელემენტი არის ამ რიცხვების უდიდესი საერთო გამყოფი. მაგალითად:

D(18, 24, 36 ) = 6.

უდიდესი საერთო გამყოფის მოსაძებნად საჭიროა ეს რიცხვები დავშალოთ მარტივ მამრავლებად, ამოვწეროთ მათი საერთო მამრავლები და გადავამრავლოთ. მაგალითად:

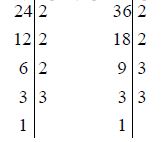
ე. ი. 24 = 2 ⋅ 2 ⋅ 2 ⋅ 3 ან 24 = 2² . 3 და 36 = 2 ⋅ 2 ⋅ 3 ⋅ 3 ან 36 = 2² . 3², ამიტომ D(24,36) = 2 ⋅ 2 ⋅ 3 = 12. რადგან 24-ისა და 36-ის გაშლაში რიცხვი 2 საერთო მამრავლად შედის 2-ჯერ, ხოლო 3 ერთხელ.

ორ ნატურალურ რიცხვს ეწოდება ურთიერთმარტივი, თუ მათი უდიდესი საერთო გამყოფი 1-ის ტოლია. ასე მაგალითად, რადგან D(18,25) = 1, ამიტომ 18 და 25 ურთიერთმარტივი რიცხვებია.

n ნატურალური რიცხვის ჯერადი ეწოდება ისეთ m ნატურალურ რიცხვს, რომელიც n-ზე იყოფა უნაშთოდ. ნებისმიერი ნატურალური რიცხვის ჯერადთა სიმრავლე უსასრულოა, მის უმცირეს ელემენტს წარმოადგენს თვით ეს რიცხვი, ხოლო უდიდესი ელემენტი არ გააჩნია. მაგალითად, 12-ის ჯერადთა სიმრავლეა {12,24,36,48, ...}.

რამდენიმე ნატურალური რიცხვის საერთო ჯერადი ეწოდება რიცხვს, რომელიც თითოეული მათგანის ჯერადს წარმოადგენს. მაგალითად, 18-ის, 24-ისა და 36-ის საერთო ჯერადებია: 72, 144, 216, ...

m, n, ..., k ნატურალური რიცხვების უმცირესი საერთო ჯერადი ეწოდება მათ საერთო ჯერადთა შორის უმცირესს და K(m, n, ..., k ) სიმბოლოთი აღინიშნება. განსახილველი რიცხვების საერთო ჯერადთა სიმრავლე წარმოადგენს მათ ჯერადთა სიმრავლეების თანაკვეთას. ეს სიმრავლე უსასრულოა, მაგრამ არსებობს მისი უმცირესი ელემენტი და იგი ამ რიცხვების უმცირესი საერთო ჯერადის ტოლია. მაგალითად:

K(18, 24, 36) = 72.

რამდენიმე რიცხვის უმცირესი საერთო ჯერადის მოსაძებნად საჭიროა ეს რიცხვები დავშალოთ მარტივ მამრავლებად, ამოვწეროთ ერთ-ერთი მათგანის ყველა მამრავლი და მივუწეროთ მათ მეორე რიცხვის ის მამრავლები, რომლებიც აკლია ამოწერილ მამრავლებს, შემდეგ მივუწეროთ მესამე რიცხვის ის მამრავლები, რომლებიც აკლია უკვე ამოწერილ მამრავლებს და ა. შ.

მოცემული რიცხვების უმცირესი საერთო ჯერადი უდრის ყველა ამოწერილ მამრავლთა ნამრავლს. მაგალითად, 24 = 2 ⋅ 2 ⋅ 2 ⋅ 3 ან 24 = 2³ . 3, 36 = 2⋅ 2 ⋅ 3 ⋅ 3 ან 36 = 2² . 3², ამიტომ K(24, 36) = 2 ⋅2 ⋅ 2 ⋅ 3 ⋅ 3 = 72 ან 2³ . 3², რადგან 24-ის 2 ⋅ 2 ⋅ 2 ⋅ 3 ან 24 = 2³ . 3 გაშლას აკლია ერთი 3-იანი 36-ის გაშლიდან.

შევნიშნოთ, რომ, თუ m,n ∈ N , მაშინ D(m,n) ⋅ K(m,n) = mn.

---

შენიშვნა: მათემატიკური ცნებები ძირითადად წარმოდგენილია ეროვნული მისაღები გამოცდებისთვის განკუთვნილი სახელმძღვანელოდან - ავტორები: ს.თოფურია, ვ.ხოჭოლავა, ნ.მაჭარაშვილი, გ. აბესაძე, ზ. მეტრეველი.

განმარტება: პროფესორ ს. თოფურიას რედაქციით მეხუთე გადამუშავებული გამოცემა.