ალბათობის კლასიკური განმარება მოითხოვს, რომ ელემენტარულ ხდომილებათა სრული სისტემა შედგებოდეს სასრული რაოდენობის ტოლშესაძლებელი ხდომილებებისგან, პრაქტიკაში კი ხშირად ვხვდები ცდებს, რომელთა ტოლშესაძლებელ შედეგთა სიმრავლე უსასრულოა. ასეთ შემთხვევაში სარგებლობენ ალბათობის გეომეტრიული განსაზღვრებით.

ვთქვათ, მოცემული გვაქვს მონაკვეთი, რომლის სიგრძე უდრის a-ს, |AB| = a და ამ მონაკვეთზე |CD| = b. ალბათობა იმისა, რომ AB მონაკვეთზე შემთხვევით შერჩეული წერტილი მოხვდეს ამ მონაკვეთზე არსებულ CD მონაკვეთზე გამოითვლება ფორმულით:

P = a/b.

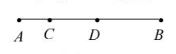
აქ AB მონაკვეთი ხდომილებათა სრული სისტემის (სივრცის) როლშია, დასახელებულ ხდომილებას AB მონაკვეთის ქვესიმრავლეს - CD მონაკვეთს ვუთანაბრებთ.

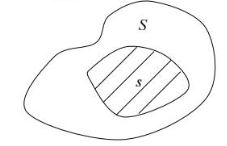
ანალოგიურად, ვთქვათ მოცემული გვაქვს S ფართობის მქონე რაიმე ბრტყელი ფიგურა და ამ ფიგურის რაიმე ნაწილი, რომლის ფართობია s. ალბათობა იმისა, რომ მოცემულ ფიგურაზე შემთხვებით შერჩეული წერტილი მოხვდება ამ ფიგურის s ფართობის მქონე ნაწილში, გამოითველბა ფორმულით:

P = s/S.

---

შენიშვნა: მათემატიკური ცნებები ძირითადად წარმოდგენილია ეროვნული მისაღები გამოცდებისთვის განკუთვნილი სახელმძღვანელოდან - ავტორები: ს.თოფურია, ვ.ხოჭოლავა, ნ.მაჭარაშვილი, გ. აბესაძე, ზ. მეტრეველი.

განმარტება: პროფესორ ს. თოფურიას რედაქციით მეხუთე გადამუშავებული გამოცემა.